Basics
Like everyone else who thinks that they're smart, I really love the concept of the Map and the Territory. The best intro to this topic is Jorge Luis Borges' On Exactitude in Science, which I'll quote in its entirety here:
...In that Empire, the Art of Cartography attained such Perfection that the map of a single Province occupied the entirety of a City, and the map of the Empire, the entirety of a Province. In time, those Unconscionable Maps no longer satisfied, and the Cartographers Guilds struck a Map of the Empire whose size was that of the Empire, and which coincided point for point with it. The following Generations, who were not so fond of the Study of Cartography as their Forebears had been, saw that that vast Map was Useless, and not without some Pitilessness was it, that they delivered it up to the Inclemencies of Sun and Winters. In the Deserts of the West, still today, there are Tattered Ruins of that Map, inhabited by Animals and Beggars; in all the Land there is no other Relic of the Disciplines of Geography.
- Suarez Miranda,Viajes devarones prudentes, Libro IV,Cap. XLV, Lerida, 1658
A Territory is an actually existing thing, and a Map is a abstraction or representation of that thing. As Borges suggests, all maps must be smaller than the territory they represent in order to be useful. If they did not, they would simply be a copy of the territory. Because they are smaller, maps must necessarily exclude some information that the territory contains. For physical maps, this means an exclusion of detail - most maps will not mark out, say, every single tree in the territory. Rather, they will label a whole region which has a high tree density as "forest," and that's good enough. I call this process of exclusion "compression," as in "the map compresses the territory."
A Lemma On Compression
A quick explainer on compression and the aspects I find most conceptually useful for people who don't program. First, there are two kinds of compression - Lossy and Lossless. The names are pretty self-explanatory: Lossless compression compresses information in a way where you can get back the original perfectly, and lossy compression only allows for an imperfect reconstruction
I think it's easiest to understand with an example. Let's say that my friend B and I are both huge fans of the artist Miranda, who's well known for all of her works being a 8 by 8 grid of squares, where each square is colored either black or white. I managed to get an exclusive online preorder of Miranda's new art book, but B doesn't own any electronic device other than a flip phone and so could not. Because of their unfortate technological situation, we also can't send each other anything but plain text messages. B of course wants to see Miranda's new art, but I can't just send them pictures, so I need to describe each artpiece textually. This is the first image in the book:

To describe this image to B, I could, if I were very dumb or wanted to annoy my friend, send B a message saying "The square in the first row and first column is white. The square in the first row and second column is white. The square in the first row and third column is white. The square in the first row and fourth column is white..." and so on until I got to "The square in the eigth row and eigth column is white." We can refer to this method of describing the image, which would obviously work for any of Miranda's art, as the Long Annoying Method. However, being a considerate friend, I just send the message "it's all white." Both the Long Annoying Method and just saying "it's all white" are Lossless forms of compression, as B will be able to perfectly recreate (in their imagination or on paper) the image from the artbook.

For the second image, I could, of course, use the Long Annoying Method. I could also say that "It's all white, except that the square in the 6th row and third column is black." Both would allow B to exactly recreate the original, and therefore are lossless. However, we now have a Lossy option. If I'm feeling lazy, or if my phone company charges by the letter for texting, I could just tell B that "There's one black square." While B wouldn't be able to make an exact copy, their best guess (an all-white image) would only be off by one square, and they would know that.

This third image is much tougher. If I want to send B a lossless representation, I don't have many options outside of the Long Annoying Method. The only better option I can come up with is to only specify the location of the black squares, since the image is mostly white, i.e. "It's all white, except the square in the third row and third column is black, and the square in the third row and sixth column is black..." and so on. This is still a really long message! Thankfully, we have lossy compression here to help. If you tell B "it's a smiley face," they'll be able to form a pretty good idea of what the image looks like (although they may not be certain of any particular square's color). There's many different options for lossy compression, with differing trade-offs for message length and description detail. For instance, you could say "it's a symmetric smiley face," or "it's a smiley face with a left eye starting at the square in the third row and third column, a right eye starting at the square in the third row and sixth column, and a mouth starting at the square in the sixth row and second column." You could also tell B that "it's mostly white." However, this is a pretty bad compression here, since the pattern in the image means we can do better for pretty much the same length.

The fourth and final image we'll be considering is the hardest of all to describe. For lossless representation, we really have no choice but the Long Annoying Method. As for lossy representation, we could tell B that "it looks like static." But this actually doesn't tell B much at all about the image! Miranda's art style allows for 18,446,744,073,709,551,616 (that's 18 billion billion) possible images, the vast majority of which will look like static. If we're being generous with the approximation, we can say we've maybe narrowed it down to a mere 17 billion billion images. Compare this to our previous lossy compressions: "There's one black square" narrows it down to 64 options, and depending on B's definition of a smiley face, "it's a smiley face" narrows it to a few hundred. Really, saying "it looks like static" is not describing a pattern in the image, but rather an image which lacks a pattern (computery people call lacking-a-pattern "entropy"). We can therefore call this image "uncompressible," since the only way to effectively describe it to B is square-by-square.
Reality Cannot Be Losslessly Compressed
For the sake of staying focused within this page, let's assume naive realism is true. This means that the stuff you observe (with your senses or a microscope or the LHC) Actually Exists, and we can call all of it Reality. If you're philosophy-brain enough to believe in a different view of Reality, then you can probably also figure out for yourself how to apply the conclusions reached here to your view. We can therefore trust science when it tells us that everything is made of molecules, which are made of atoms, which are made of electrons and hadrons, which are made of quarks, which we don't know the composition of.
When we were talking about Miranda's art, we were compressing and sending B the information contained within the book, that is, the idea formed in one's brain after looking at the images. But now, let's say B has one piece of technology other than their flip phone: a highly advanced replicator, à la Star Trek. They want to use it to not just copy the art, but to make themselves a copy of the book, and specifically a lossless copy. Note that this time, we're compressing not an image or a description of an image, but rather the book itself, the actual physical object. For them to create an exact copy of the book, we'd have to tell B the state (e.g. location, momentum, spin) of every single elementary particle within the book. Now, it turns out that both the replicator and the possibility of describing our book exactly with a text message are prohibited by the no-teleportation theorem, so any description and recreation must be imperfect, i.e. lossy.
However, we don't need the no-teleportation theorem to prove that B won't get their lossless copy. Suppose that quantum physics is all a scam made up by Big Science to sell more science. In this hypothetical reality, particles have exact locations, measurement doesn't change the thing being measured, and velocity and position can be measured simultaneously with no uncertainty. Even then, we still can't give B an exact copy. The position and velocity you measure for each particle in the book must be measured to a finite number of significant figures, since your text message must be finitely long (and you couldn't read the display of an infinite-precision measuring device anyways). Since you can always include more significant figures (i.e. make your measurements more precise), whatever precision you end up deciding on can't be a perfect representation, because a better one exists. (Side note: if you're trying to get out of this by appealing to the Planck length as a "maximum precision," it doesn't work because 1. that puts you right back into quantum-land, where the no-teleportation and no-cloning theorems prevent this, and 2. the Planck length represents the smallest scale we can make predictions about with our current understanding of physics, not some fundamental resolution of reality).
A third argument against a perfect, lossless compression of reality is that physics is never complete. The history of physics (and also other science afaik) can be oversimplified as this cycle:
While our current understanding of physics is very much still in this cycle (current problems include quantum gravity, dark matter, etc.), one can imagine a physics that seems to break this cycle - say one where no problems have arisen for a millenium. Even in this case, physics would not be complete, and we would still have physicists searching for possible problems in the accepted theories, or new scenarios outside of the realms they describe. Proving empirically that something does not exist is impossible, and so even if physics were to arrive at a final and perfect knowledge, we wouldn't be aware it had, since that would mean knowing that there does not exist a problem in that theory. Since a perfect physics is required to know what properties make up a complete, perfect description of an object, and no perfect physics is possible, no complete and perfect (read: lossless) description is possible.
Who Cares, Get A Job
While this may seem like stupid pedantry about an imaginary replicator device, everything discussed so far has significant implications. If it's impossible to describe an existing object losslessly, then that means that every time you perceive something with your senses, measure it with some instrument, or describe it to someone else, you're doing a lossy compression. This in itself is something interesting to pay attention to: how are you compressing it? What information is important and what gets culled? For example, normally when describing an event we only mention the people or objects directly involved, and only mention how they moved or interacted. Unless especially relevant, things like what each person was wearing or when they breathed are discarded. When doing a scientific experiment, you can only measure so many things, compressing some aspects of the situation out of the picture and out of mention in your eventual paper. This is where a lot of error can sneak in, because compressing out anything that significantly effects your dependent variable makes the whole experiment worthless.
However, what I'm most interested in is the compression that occurs between the brain's sensory neurons and the "conscious mind." While it doesn't nessecarily follow from what I've proven above that there is compression here, there's tremendous evidence from psychology showing that not only does that compression exist, it's absolutely massive. My favorite example is The Invisible Gorilla, where half of the people instructed to count basketball passes in a video missed a person in a gorilla suit very obviously stroll into the middle of the screen, stand there for a few seconds, and leave (the actual peer-reviewed paper can be found here). When focusing on the players, everything else in the video is compressed out, including the gorilla. Since your visual field certainly includes the entire video frame, we know the viewer's optic nerve registered the presence of the gorilla. However, it couldn't have made its way to the "conscious mind," or else the viewer would have wondered what the gorilla was doing there and remembered its presence. The compression therefore happens somewhere in the middle. This compression is very much influenced by conscious thoughts - after all, it only compressed out the gorilla because the viewer was consciously focusing on counting passes. A casual observer who wasn't trying to count (we could say they're running the "default human compression algorithm") would certainly notice the gorilla.
The Map Changes The Territory
One of the best maps I've ever seen is this one:
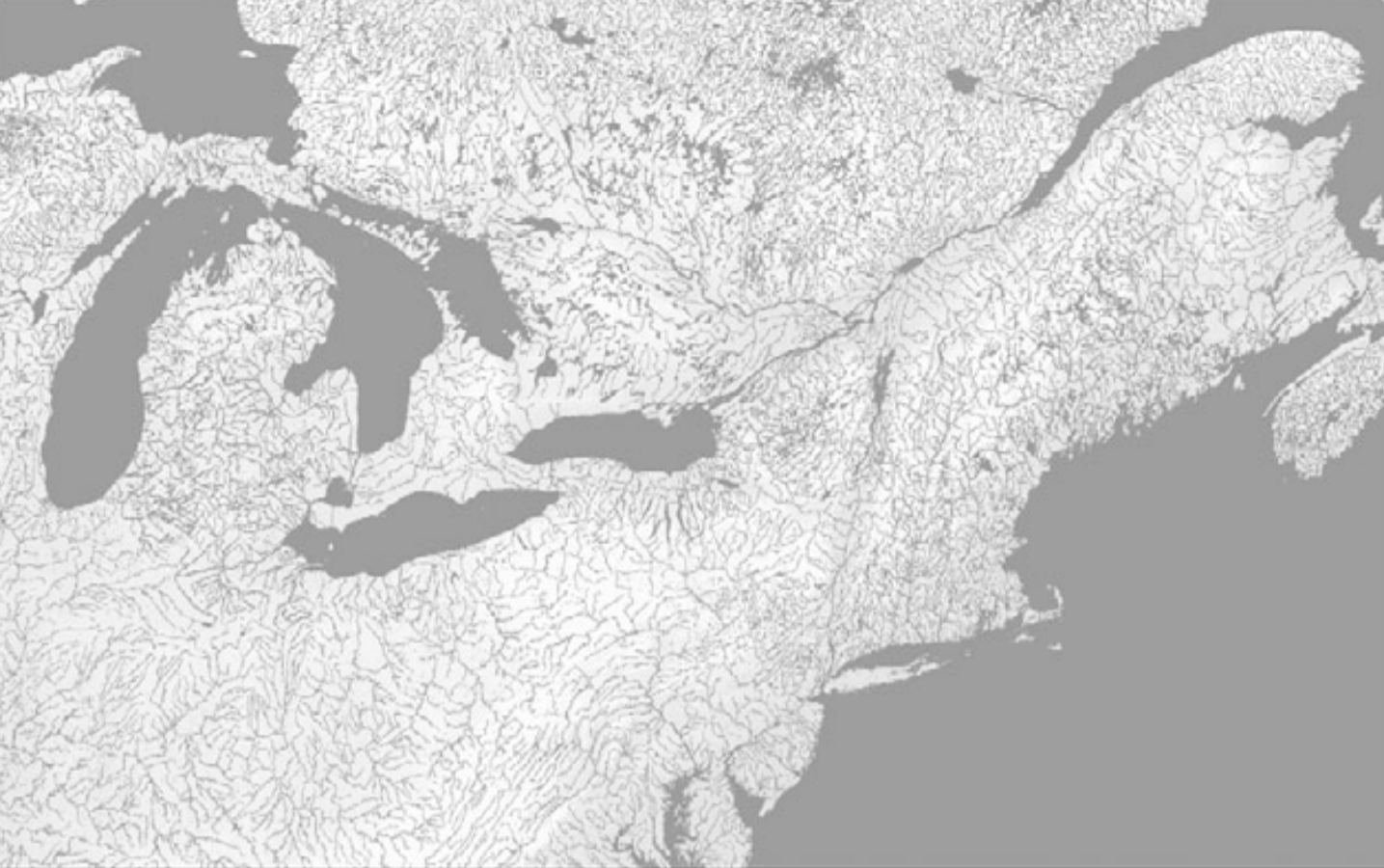
It's from The Common Pot, by Lisa Brooks. The place I grew up is on this map, so naturally when I first saw it I tried to find my town, and was pretty far off. I know the names of the rivers I was looking for, but I couldn't find them by shape and intersection alone, despite this map being way more detailed than the normal political-boundaries-only map. It made me realize how little attention I paid to the rivers around me - I had seen these rivers, hiked along and across them, and even kayaked down some of them. All the information I needed to find my home on the river map had entered my eyes at some point, but because I never thought to navigate by river, to use the rivers as my map, I had compressed it all away. If I had grown up seeing that river-map everywhere instead of a political map, then the experience I had when I saw those rivers in person would have been vastly different. Because the brain compresses in between the senses and the conscious mind, the map you use changes the territory you perceive.
This is not a metaphor. Since the only way "you" can get any information about the Real World is through the sense-compression-consciousness pipeline, changing the compression might as well be changing reality. The way that we talk about this phenomenon also reflects that it is changing reality - for example, that "when you learn a new word you'll hear it three times in the next week." Learning that new word brings it front and center on your map, where before the actual sound of the word may have been compressed out and replaced with the concept of "word to guess from context." Manifestation is another example: the manifestation rituals (e.g. writing down the thing you want over and over) serve to make whatever you're trying to manifest a major part of your map, and so nothing related to what you're manifesting (a mention of it in passing, a subtle opportunity to make it happen, etc.) will get compressed. Your reality therefore actually contains more opportunities and mentions of what you're manifesting! And of course, more opportunites make it more likely to happen, and so manifesting works. I think there's also something to be said here about the placebo effect, especially for psychiatric medicine, but that would require research and I'm lazy is left as an exercise for the reader.